From Psychology to Machine Learning : The Evolution of Diffusion Models and Their Impact on Decision-Making :
The growth of the Diffusion Model can be attributed to the recent breakthrough in the field of AI generative artworks. In this essay, I'll show you how it works using illustrative graphics.
Overview
The training of the Diffusion Model can be divided into two parts:
Forward Diffusion Process - add noise to the image.
Reverse Diffusion Process - remove noise from the image.
Forward Diffusion Process :

The forward diffusion method progressively adds Gaussian noise to the input picture x0, for a total of T steps. The technique will generate a series of noisy picture samples x1,..., x T.
When T, the resultant image will be fully noisy, as if it were sampled from an isotropic Gaussian distribution.
Instead of creating an algorithm to add noise to the picture repeatedly, we may use a closed-form formula to directly sample a noisy image at a specified time step t.
Closed-Form Formula
The closed-form sampling formula can be derived using the Reparameterization Trick.

With this trick, we can express the sampled image xₜ as follows:
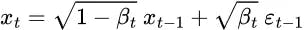
Then we can expand it recursively to get the closed-form formula:

Note: All the ε are i.i.d. (independent and identically distributed) standard normal random variables. It is important to distinguish them using different symbols and subscripts because they are independent and their values could be different after sampling.
But how do we jump from line 4 to line 5?
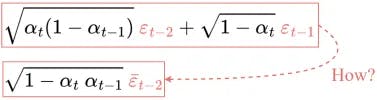
Some people find this step difficult to understand. Here I will show you how it works:

Let’s denote these two terms using X and Y. They can be regarded as samples from two different normal distributions. i.e. X ~ N(0, αₜ(1-αₜ₋₁)I) and Y ~ N(0, (1-αₜ)I).
Recall that the sum of two normally distributed (independent) random variables is also normally distributed. i.e. if Z = X + Y, then Z ~ N(0, σ²ₓ+σ²ᵧ).
Therefore we can merge them and express the merged normal distribution in the reparameterized form. This is how we combine the two terms.
Repeating these steps will give us the following formula which depends only on the input image x₀:
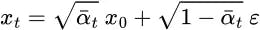
Now we can directly sample xₜ at any time step using this formula, and this makes the forward process much faster.
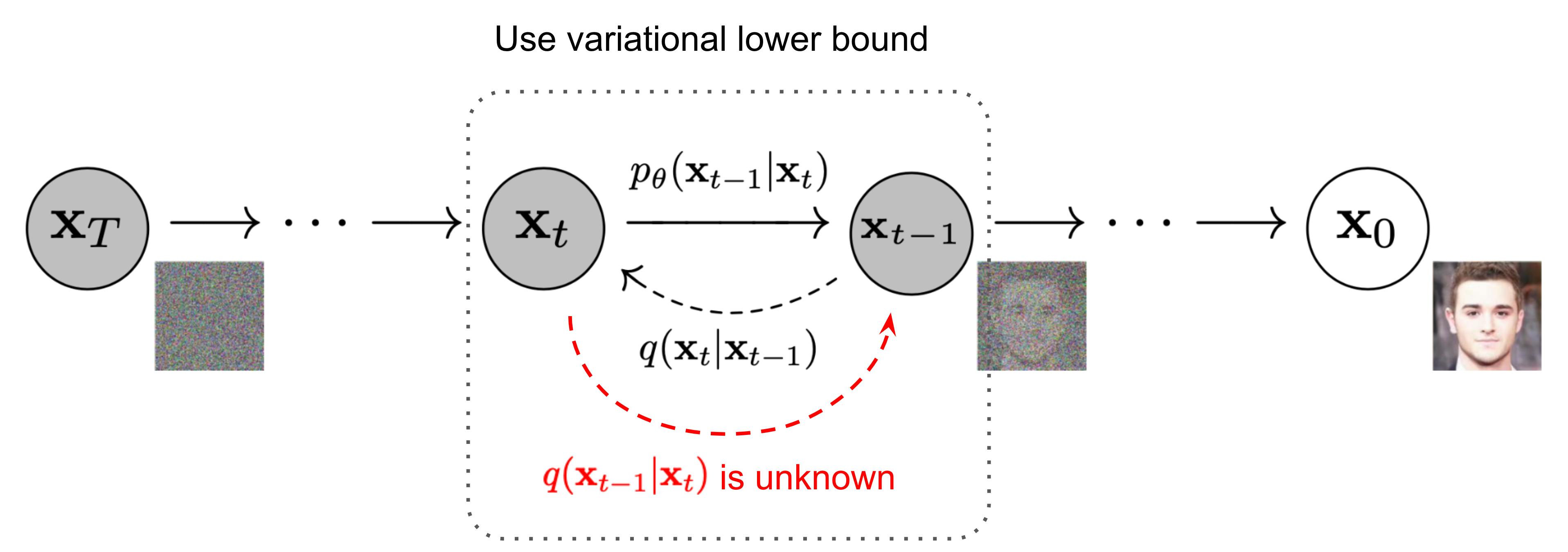
Reverse Diffusion Process :

Unlike the forward process, we cannot use q(xₜ₋₁|xₜ) to reverse the noise since it is intractable (uncomputable).
Thus we need to train a neural network pθ(xₜ₋₁|xₜ) to approximate q(xₜ₋₁|xₜ). The approximation pθ(xₜ₋₁|xₜ) follows a normal distribution and its mean and variance are set as follows:

Loss Function: We can define our loss as a Negative Log-Likelihood :
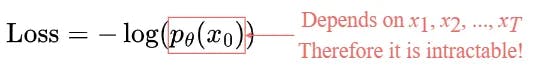
This setup is very similar to the one in VAE. instead of optimizing the intractable loss function itself, we can optimize the Variational Lower Bound.
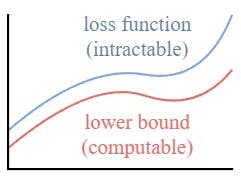
By optimizing a computable lower bound, we can indirectly optimize the intractable loss function.

By expanding the variational lower bound, we found that it can be represented with the following three terms:
- L_T: Constant term
Since q has no learnable parameters and p is just a Gaussian noise probability, this term will be a constant during training and thus can be ignored.
- Lₜ₋₁: Stepwise denoising term
This term compares the target denoising step q and the approximated denoising step pθ.
Note : That by conditioning on x₀, the q(xₜ₋₁|xₜ, x₀) becomes tractable.

After a series of derivations, the mean μ̃ₜ of q(xₜ₋₁|xₜ, x₀) is shown above.
To approximate the target denoising step q, we only need to approximate its mean using a neural network. So we set the approximated mean μθ to be in the same form as the target mean μ̃ₜ (with a learnable neural network εθ):
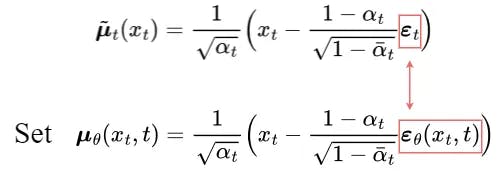
The comparison between the target mean and the approximated mean can be done using a mean squared error (MSE):
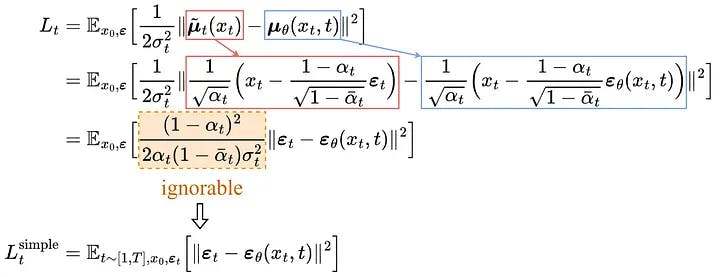
Experimentally, better results can be achieved by ignoring the weighting term and simply comparing the target and predicted noises with MSE.
So, it turns out that to approximate the desired denoising step q, we just need to approximate the noise εₜ using a neural network εθ.
- L₀: Reconstruction term
This is the reconstruction loss of the last denoising step and it can be ignored during training for the following reasons:
It can be approximated using the same neural network in Lₜ₋₁. Ignoring it makes the sample quality better and makes it simpler to implement.
Simplified Loss
So the final simplified training objective is as follows:
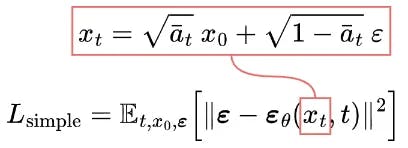
We find that training our models on the true variational bound yields better codelengths than training on the simplified objective, as expected, but the latter yields the best sample quality. [2]
The U-Net Model
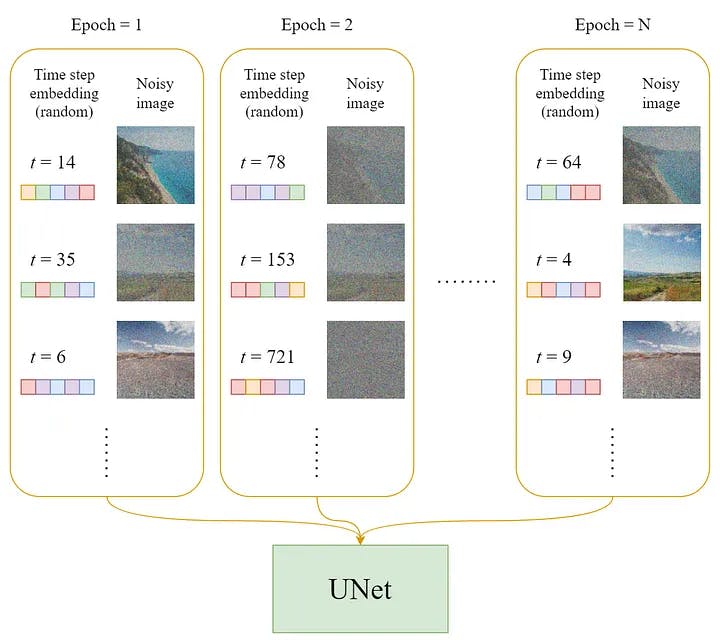
Dataset
In each epoch:
A random time step t will be selected for each training sample (image).
Apply the Gaussian noise (corresponding to t) to each image.
Convert the time steps to embeddings (vectors).
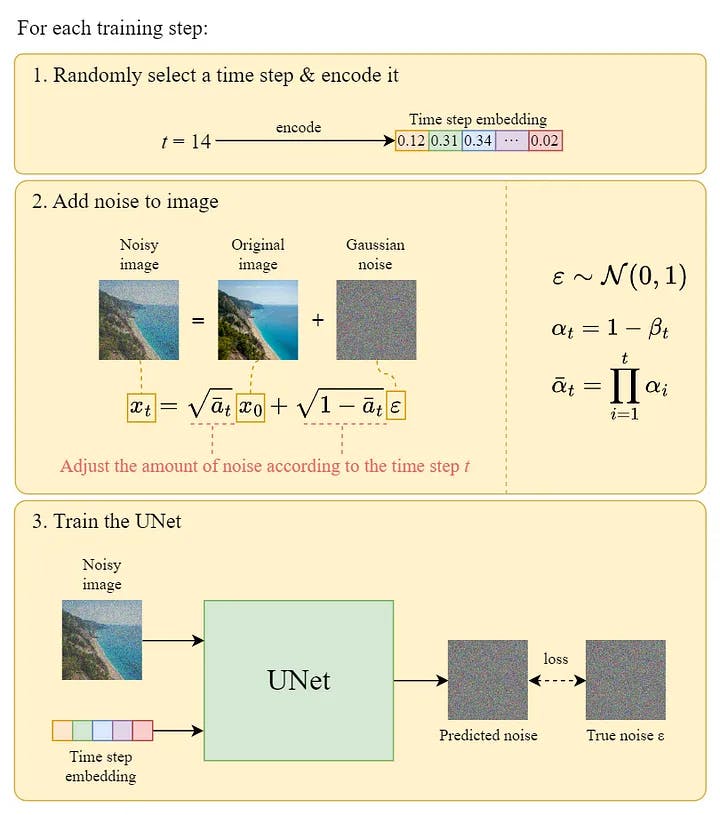
Training

The official training algorithm is as above, and the following diagram is an illustration of how a training step works:
Reverse Diffusion :

We can generate images from noises using the above algorithm. The following diagram is an illustration of it:
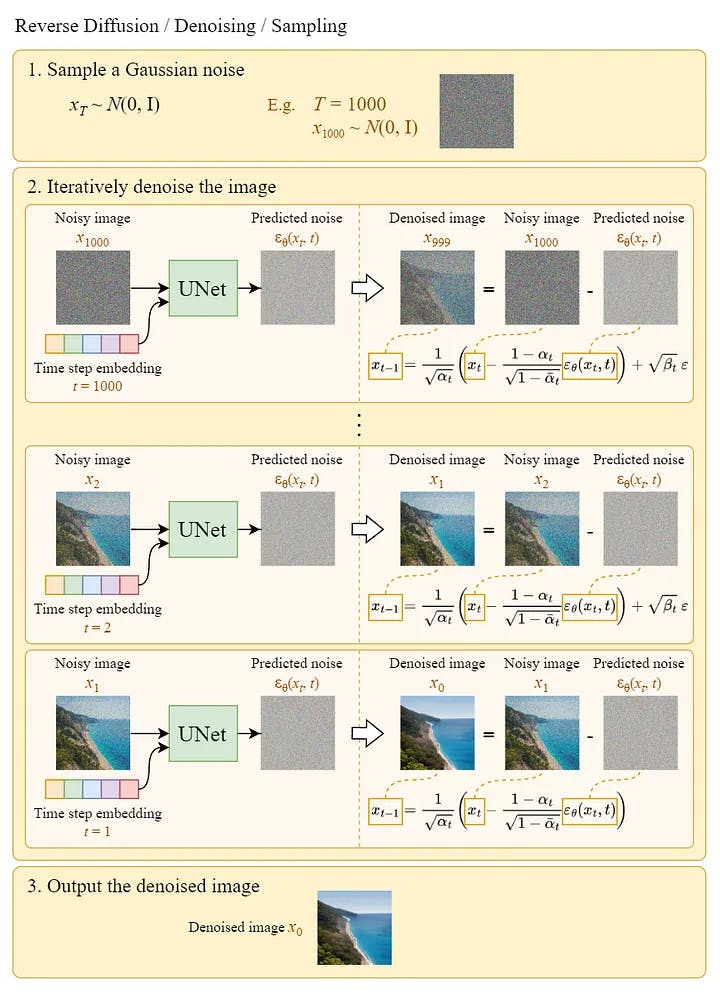
Note that in the last step, we simply output the learned mean μθ(x₁, 1) without adding the noise to it.
Summary Here are some main takeaways from this article:
The Diffusion model is divided into two parts: forward diffusion and reverse diffusion.
The forward diffusion can be done using the closed-form formula.
The backward diffusion can be done using a trained neural network.
To approximate the desired denoising step q, we just need to approximate the noise εₜ using a neural network εθ.
Training on the simplified loss function yields better sample quality.
Thank you !
